LCT Note

Veröffentlicht am | Edited on

LCT Note

Preface

准备学个数据结构来回升一下状态。LCT的题很多

前置知识实链剖分，Splay，势能分析。

Splay以前没写过具体的会详细说明。

有个大胆的想法，我准备把之前关于Splay的介绍都放过来，呈现一个更加完善的学习笔记。

原始论文From Tarjan and else…

dynamic-trees.pdf

还参考了

https://www.cnblogs.com/candy99/p/6271344.html

https://oi-wiki.org/ds/lct/

大概要学到明天

动态树原始问题：

维护一个森林, 支持删除某条边，加⼊某条边，并保证加边，删边之后仍是森林。我们要维护这个森林的一些信息。
一般的操作有两点连通性，两点路径权值和，连接两点和切断某条边、修改信息等。

可以解决这些问题：

  1. 查询一个点的父亲
  2. 查询一个点所在的树的根
  3. 修改某个节点的权
  4. 向从某个节点到它所在的树的根的路径上的所有的节点的权增加一个数
  5. 查询从某个节点到它所在的树的根的路径上的所有的节点的权的最小值
  6. 把一棵树从某个节点和它的父亲处断开，使其成为两棵树
  7. 让一棵树的根成为另一棵树的某个节点的儿子，从而合并这两棵树
  8. 把某棵树的根修改为它的某个节点
  9. 查询在同一棵树上的两个节点的LCA（动态LCA）
  10. 修改以某个节点为根的子树的所有节点的权
  11. 查询以某个节点为根的子树的所有节点的权的最小值

注意涉及到子树的问题可能需要一些补充和拓展（比如AAA树甚至Top Tree），在将来会补充。

前置知识篇

实链剖分

对于每个点选中一个重儿子，其他为轻儿子。

具体好在哪里还是看后面吧。。

Splay

回家后补上完整的学习资料。

Splay基本操作

变量声明：

f[i]表示i的父结点，

表示i的左儿子，

表示i的右儿子 , $key_i$表示i的关键字（即结点i代表的那个数字），$cnt_i$表示$i$结点的关键字出现的次数（相当于权值），$size_i$表示包括i的这个子树的大小；$sz$为整棵树的大小，$root$为整棵树的根。

【clear操作】

将当前点的各项值都清0（用于删除之后）,时间复杂度$O(1)$

1
2
3
inline void clear(int x){
     ch[x][0]=ch[x][1]=f[x]=cnt[x]=key[x]=size[x]=0;
}

【get操作】

判断当前点是它父结点的左儿子还是右儿子，时间复杂度$O(1)$

1
2
3
inline int get(int x){
     return ch[f[x]][1]==x;
}

【update操作】：

更新当前点的size值（用于发生修改之后） ,时间复杂度$O(1)$

1
2
3
4
5
6
7
inline void update(int x){
     if (x){
          size[x]=cnt[x];
          if (ch[x][0]) size[x]+=size[ch[x][0]];
          if (ch[x][1]) size[x]+=size[ch[x][1]];
     }
}

【旋转操作】：

务必完全理解这个操作，这是平衡树最重要的，复杂度得到保证的操作

【rotate操作图文详解】

img

这是原来的树，假设我们现在要将D结点rotate到它的父亲的位置。

  • step 1：

找出D的父亲结点（B）以及父亲的父亲（A）并记录。判断D是B的左结点还是右结点。

  • step 2：

我们知道要将Drotate到B的位置，二叉树的大小关系不变的话，B就要成为D的右结点了没错吧？

咦？可是D已经有右结点了，这样不就冲突了吗？怎么解决这个冲突呢？

我们知道，D原来是B的左结点，那么rotate过后B就一定没有左结点了对吧，那么正好，我们把G接到B的左结点去，并且这样大小关系依然是不变的，就完美的解决了这个冲突。如下图。

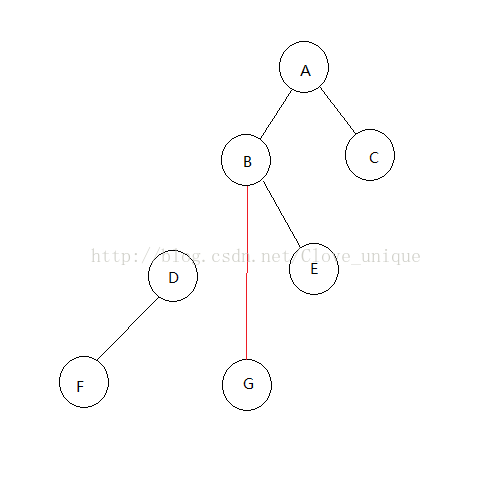
Splay2

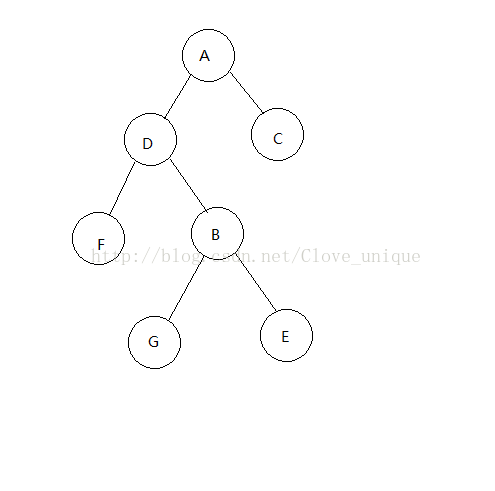
Splay3

这样我们就完成了一次rotate，如果是右儿子的话同理。step 2的具体操作：

我们已经判断了D是B的左儿子还是右儿子，设这个关系为K；将D与K关系相反的儿子的父亲记为B与K关系相同的儿子（这里即为D的右儿子的父亲记为B的左儿子）；将D与K关系相反的儿子的父亲即为B（这里即为把G的父亲记为B）；将B的父亲即为D；将D与K关系相反的儿子记为B（这里即为把D的右儿子记为B）；将D的父亲记为A。

最后要判断，如果A存在（即rotate到的位置不是根的话），要把A的儿子即为D。

显而易见，rotate之后所有牵涉到变化的父子关系都要改变。以上的树需要改变四对父子关系，BG DG BD AB，需要三个操作（BG BD AB）。

  • step 3：update一下当前点和各个父结点的各个值

以前Treap我写旋转都是左旋右旋分开写。。想必看了上面的图不难发现规律并把两个写在一起。

并且不要漏了某些父子关系忘了修改，显然比递归传址维护父子麻烦点。

1
2
3
4
5
6
7
8
9
inline void rotate(int x){
     int old=f[x],oldf=f[old],which=get(x);
     ch[old][which]=ch[x][which^1];f[ch[old][which]]=old;
     f[old]=x;ch[x][which^1]=old;
     f[x]=oldf;
     if (oldf)
          ch[oldf][ch[oldf][1]==old]=x;
     update(old);update(x);
}

接下来是Splay操作，大致和Treap一样但是好像需要分更多情况讨论一下。

【Splay操作】

其实splay只是rotate的发展。伸展操作只是在不停的rotate，一直到达到目标状态。如果有一个确定的目标状态，也可以传两个参。此代码直接splay到根。

splay的过程中需要分类讨论，如果是三点一线的话（x，x的父亲，x的祖父）需要先rotate x的父亲，否则需要先rotate x本身（否则会形成单旋使平衡树失衡）（这东西还需要再去了解一下）

1
2
3
4
5
6
inline void splay(int x){
     for (int fa;(fa=f[x]);rotate(x))
          if (f[fa])
               rotate((get(x)==get(fa)?fa:x));
     root=x;
}

【insert操作】

其实插入操作是比较简单的，和普通的二叉查找树基本一样。

step 1：如果root=0，即树为空的话，做一些特殊的处理，直接返回即可。

step 2：按照二叉查找树的方法一直向下找，其中：

如果遇到一个结点的关键字等于当前要插入的点的话，我们就等于把这个结点加了一个权值。因为在二叉搜索树中是不可能出现两个相同的点的。并且要将当前点和它父亲结点的各项值更新一下。做一下splay。

如果已经到了最底下了，那么就可以直接插入。整个树的大小要+1，新结点的左儿子右儿子（虽然是空）父亲还有各项值要一一对应。并且最后要做一下他父亲的update（做他自己的没有必要）。做一下splay。！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
inline void insert(int v){
     if (root==0) 
     {sz++;ch[sz][0]=ch[sz][1]=f[sz]=0;key[sz]=v;cnt[sz]=1;size[sz]=1;root=sz;return;}
     int now=root,fa=0;
     while (1){
          if (key[now]==v){
               cnt[now]++;update(now);update(fa);splay(now);break;
          }
          fa=now;
          now=ch[now][key[now]<v];
          if (now==0){
               sz++;
               ch[sz][0]=ch[sz][1]=0;key[sz]=v;size[sz]=1;
               cnt[sz]=1;f[sz]=fa;ch[fa][key[fa]<v]=sz;
               update(fa);
               splay(sz);
               break;
          }
     }
}

【find操作】

查询x的排名

初始化：ans=0，当前点=root

和其它二叉搜索树的操作基本一样。但是区别是：

如果x比当前结点小，即应该向左子树寻找，ans不用改变（设想一下，走到整棵树的最左端最底端排名不就是1吗）。

如果x比当前结点大，即应该向右子树寻找，ans需要加上左子树的大小以及根的大小（这里的大小指的是权值）。

不要忘记了再splay一下

1
2
3
4
5
6
7
8
9
10
11
12
13
inline int find(int v){
     int ans=0,now=root;
     while (1){
          if (v<key[now])
               now=ch[now][0];
          else{
               ans+=(ch[now][0]?size[ch[now][0]]:0);
               if (v==key[now]) {splay(now);return ans+1;}
               ans+=cnt[now];
               now=ch[now][1];
          }
     }
}

【findx操作】

找到排名为x的点

初始化：当前点=root

和上面的思路基本相同：

如果当前点有左子树，并且x比左子树的大小小的话，即向左子树寻找；

否则，向右子树寻找：先判断是否有右子树，然后记录右子树的大小以及当前点的大小（都为权值），用于判断是否需要继续向右子树寻找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline int findx(int x){
     int now=root;
     while (1){
          if (ch[now][0]&&x<=size[ch[now][0]])
               now=ch[now][0];
          else{
               int temp=(ch[now][0]?size[ch[now][0]]:0)+cnt[now];
              if (x<=temp){
                  splay(now);
                  return key[now];
              }
               x-=temp;now=ch[now][1];
          }
     }
}

【pre/next操作】

这个操作十分的简单，只需要理解一点：在我们做insert操作之后做了一遍splay。这就意味着我们把x已经splay到根了。求x的前驱其实就是求x的左子树的最右边的一个结点，后继是求x的右子树的左边一个结点（想一想为什么？）

1
2
3
4
5
6
7
8
9
10
11
inline int pre(){
     int now=ch[root][0];
     while (ch[now][1]) now=ch[now][1];
     return now;
}
 
inline int next(){
     int now=ch[root][1];
     while (ch[now][0]) now=ch[now][0];
     return now;
}

【del操作】

删除操作是最后一个稍微有点麻烦的操作。

step 1：随便find一下x。目的是：将x旋转到根。

step 2：那么现在x就是根了。如果cnt[root]>1，即不只有一个x的话，直接-1返回。

step 3：如果root并没有孩子，就说名树上只有一个x而已，直接clear返回。

step 4：如果root只有左儿子或者右儿子，那么直接clear root，然后把唯一的儿子当作根就可以了（f赋0，root赋为唯一的儿子）

剩下的就是它有两个儿子的情况。

step 5：我们找到新根，也就是x的前驱（x左子树最大的一个点），将它旋转到根。然后将原来x的右子树接到新根的右子树上（注意这个操作需要改变父子关系）。这实际上就把x删除了。不要忘了update新根。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
inline void del(int x){
     int whatever=find(x);
     if (cnt[root]>1) {cnt[root]--;update(root);return;}
     //Only One Point
     if (!ch[root][0]&&!ch[root][1]) {clear(root);root=0;return;}
     //Only One Child
     if (!ch[root][0]){
          int oldroot=root;root=ch[root][1];f[root]=0;clear(oldroot);return;
     }
     else if (!ch[root][1]){
          int oldroot=root;root=ch[root][0];f[root]=0;clear(oldroot);return;
     }
     //Two Children
     int leftbig=pre(),oldroot=root;
     splay(leftbig);
     f[ch[oldroot][1]]=root;
     ch[root][1]=ch[oldroot][1];
     clear(oldroot);
     update(root);
     return;
}

Splay区间翻转

显然在Splay基本操作讲清楚了，又有如下几个问题

  • 求x的前驱其实就是求x的左子树的最右边的一个结点，后继是求x的右子树的左边一个结点（想一想为什么？）

答案非常简单，如果我们把x先插入旋转到根上，左子树全部不大于x，右子树全部不小于x，左子树最右边节点保证在左子树内最大，右子树最左边节点同理。不大于x的最大值与不小于x的最小值就是前驱后继的定义（不过有可能重复）。

  • 为什么Splay提取一个区间是将区间左端点的前驱旋转至根，右端点后继旋转至根的右儿子，右儿子的左子树就是区间呢？

这个问题非常重要，是区间操作的基本原理。

显然第一次旋转后左端点在根的右子树，第二次旋转后右端点在根的右儿子的左子树，在区间(L,R)内，任何一个节点既不能在根的左子树（BST性质，它们大于左端点），又不能在根的右儿子的右子树（同样不能大于右端点），因此整个闭区间所有节点都在根的右儿子的左子树内了！

  • 还有个我认为非常难证明的问题，就是为什么懒标记是正确的。。。线段树懒标记正确在于它的形态是不会发生改变的，显然每个节点代表了固定的区间。但是Splay显然作为子树的根的节点只是临时的，那会不会造成错误的标记呢？

这个问题让我想了半天。实际上是这样的。考虑暴力Splay翻转区间是从根的右儿子的左儿子u开始，对于每个节点我们都交换左右子树，这相当于一组操作。显然只要我们没有访问一个点，它的子树交不交换并没有什么区别。也就是说我们没必要重复交换，只需要在访问的时候确保进行操作并下传标记即可。那么对于当前根，我们交换子树并给这个点打上标记，后面只要访问到这个点就下推标记并操作，这样确保每个该翻转的子树翻转了，也能优化复杂度（具体严格复杂度证明以后补上吧）。

总结一下这个问题就是：只要子树不旋转，这个子树的根就不pushdown，这其实就是懒标记的思想，尽管Splay不像线段树形态固定，只要遵循这一原则就一定不会出错。

上述问题都理解了的话，一遍写过Splay十分轻松（97行）

那么区间操作也不是很难了，我们只需要在提取的区间根节点交换左右儿子并打上懒标记即可。

区间操作Splay（只有翻转操作，其它的也差不多）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 500005
#define INF 0x7ffffff
#define ls s[node][0]
#define rs s[node][1] 
int f[maxn] , s[maxn][2] , key[maxn] , val[maxn] , n , m , sz[maxn] , rev[maxn] , tot, root;
inline void update(int node)
{
	if(node){
		sz[node] = 1;
		sz[node] += sz[ls];
		sz[node] += sz[rs];
	}
}
inline void pushdown(int node)
{
	if(node && rev[node])
	{
		rev[node] = 0;
		rev[ls] ^= 1;
		rev[rs] ^= 1;
		std::swap(ls , rs);
	}
}
inline int get(int node){
	return s[f[node]][1] == node;
}
inline void rotate(int node)
{
	int fx = f[node] , ffx = f[fx] , son = get(node);
	s[fx][son] = s[node][son^1] , f[s[node][son^1]] = fx;
	f[node] = ffx ;
   	if(ffx)	s[ffx][s[ffx][1]==fx] = node;
	s[node][son^1] = fx , f[fx] = node;
	update(node) , update(fx) ;
}
inline void splay(int x , int pos)
{
	for(int fx ; (fx = f[x]) != pos ; rotate(x))
		if(f[fx] != pos)
			rotate((get(x) == get(fx))? fx : x);
	if(!pos) root = x;
}
int build(int l , int r , int fx)
{
	if(l > r) return 0;
	int mid = l + r >> 1 , node = ++tot;
	key[node] = val[mid];
	f[node] = fx;
	ls = build(l , mid - 1 , node);
	rs = build(mid + 1 , r , node);
	update(node);
	return node;
}
int find(int k)
{
	int node = root;
	while(node)
	{
		pushdown(node);
		if(k <= sz[ls]) node = ls;
		else{
			k -= sz[ls] + 1;
			if(!k) return node;
			node = rs;
		}
	}
	return -1;
}
void print(int node)
{
	pushdown(node);
	if(ls) print(ls);
	if(key[node] != -INF && key[node] != INF) printf("%d ",key[node]);
	if(rs) print(rs);
}
int main()
{
	scanf("%d%d",&n,&m);
	val[1] = -INF , val[n+2] = INF;
	for(int i = 2 ; i <= n + 1 ; ++i)
		val[i] = i-1;
	root = build(1 , n + 2 , 0);
	while(~(--m))
	{
		int l , r;
		scanf("%d%d",&l,&r);
		int posl = find(l) , posr = find(r+2);
		splay(posl , 0);
		splay(posr , posl);
		rev[s[s[root][1]][0]] ^= 1;
	}
	print(root);
}

摊还分析与Splay的复杂度证明

势能分析并不是难在推导过程，那个其实非常简单，只需要把对应操作后的状态用势能函数表示一下，然后最后求和保证能消去即可。

难在理解势能函数。为什么势能函数是正确的，势能的单位不影响最后的结果，操作复杂度与势能的改变并不对应？

势能分析并不将预付代价表示为数据结构中特定对象的信用，而是表示为势能。一个势能函数将一个数据结构的状态映射为一个实数。

如果设$i$时刻的数据结构状态是$D_i$，势能函数映射的势能是$\phi(D_i)$，

一次操作的实际代价$\hat ci = c_i + \phi(D_i) - \phi(D{i-1})$

当$\phi(Di)-\phi(D{i-1})$大于0，意味着提前支付了费用，相反的，则意味着少支付了费用。

以前我正好弄反了，结果就学不会了

不过知道了正确定义后反而感觉没法感性理解了，那就再学习下吧

进入Splay证明正式阶段

几乎抄袭自Mr.Spade

本文用势能法证明Splay的均摊复杂度，对Splay的具体操作不进行讲述。

为了方便本文的描述，定义如下内容：

在文中我们用$T$表示一棵完整的Splay，并（不严谨地）用$|T|$表示$T$这棵Splay的节点数目。

如无特殊说明，小写英文字母（如x，y，z）在本文中表示T的一个节点，并（不严谨地）用$|x|$表示以节点$x$为根的子树的大小，$x \in T$表示节点x在T中。

一般我们默认$x′$代表节点$x$在经过了上下文中描述的操作以后的状态，因此对应的x代表之前的状态。

我们用$\phi(T)$表示整棵Splay的势能函数，$\phi(x)$则表示节点x对T贡献的势能。

我们这么定义势能函数：

$\phi(x) = log_2|x|$

$\Phi(T) = \sum_{x \in T}\phi(x)$

可以发现，对于任意时刻，因为$|x|≥1$，因此$log|x|≥0$，从而得到$\Phi(T)≥0$，因此势能函数是合法的。同时$\forall |x|≤|T|$，因此我们总有$\Phi(T)≤|T|log|T|$。这个上界是比较松的，但是对我们的分析没有影响。

下面考虑一次伸展操作对于势能函数的影响。由于我们可以把从根向下查找的代价计算到伸展过程中对应的旋转操作上，此时旋转操作复杂度不变，只是常数增大，从而忽略了查找对复杂度的影响。我们可以简单地通过增大势的单位来支配隐藏在操作中的常数。因此我们只需证明对于一次伸展操作的所有旋转操作，其复杂度是均摊$O(log|T|)$的，我们就完成了对Splay复杂度的证明。

1、zig操作

img

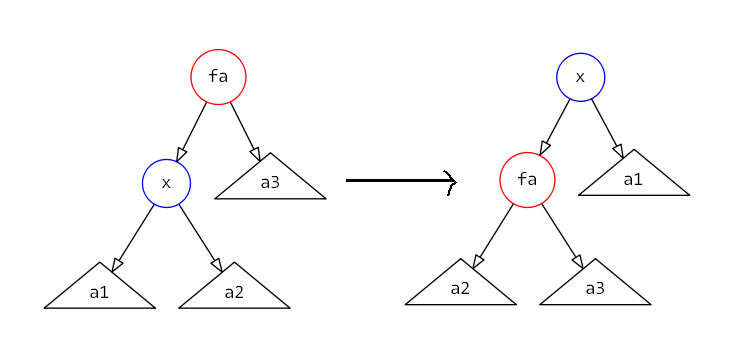
由于zag操作与zig相似，因此只需要证明zig即可。

假设我们zig的对象是x，其父亲为y，显然在旋转以后，只有x和y的子树大小发生了变化。因此势能变化量为：

$\delta \phi(T)=\phi(x′)+\phi(y′)−\phi(x)−\phi(y)$

显然$\phi(x′)=\phi(y)$，且\phi(x′)≥\phi(y′)，因此消去$\phi(x′)$与$\phi(y)$，并将$\phi(y′)$替换为$\phi(x′)$，有：

$\delta \phi(T)≤\phi(x′)−\phi(x)$

因此zig操作的均摊代价为$O(1+\phi(x′)−\phi(x))$，其中$O(1)$代表旋转操作本身的复杂度，而在一次伸展操作中也只会有一次zig操作，因此这额外的$O(1)$代价不会对分析造成影响，因此我们可以只关心其中的$O(\phi(x′)−\phi(x))$。

2、zig−zig操作

img

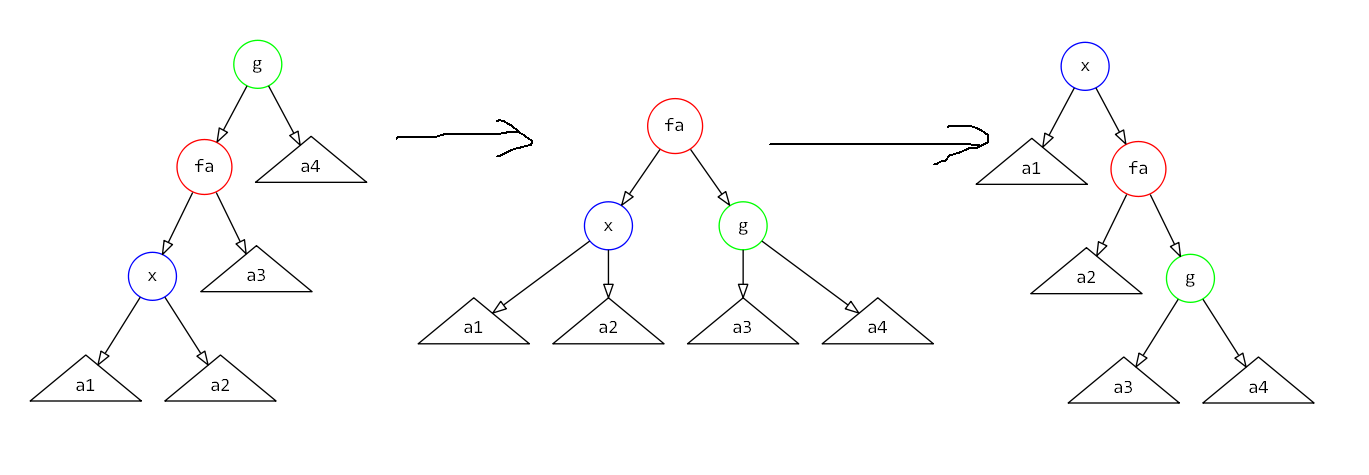
由于zag−zag操作与zig−zig相似，因此只需要证明zig−zig即可。

假设我们zig−zig的对象是x，其父亲为y，其祖父为z，与zig操作类似，势能变化量为：

$\delta \phi(T)=\phi(x′)+\phi(y′)+\phi(z′)−\phi(x)−\phi(y)−\phi(z)$

同样地，由于$\phi(x′)=\phi(z)$，因此将它们消去：

$\delta \phi(T)=\phi(y′)+\phi(z′)−\phi(x)−\phi(y)$

而我们又有$\phi(x′)≥\phi(y′)，\phi(x)≤\phi(y)$，因此有：

$\delta \phi(T)≤\phi(x′)+\phi(z′)−2\phi(x)$

推到这里，我们先来做一个小工作，来证明$\phi(x)+\phi(z′)−2\phi(x′)$（注意与上面的式子不一样）的值不大于−1。

假设$|x|=a，|z′|=b$，那么我们有：

$\phi(x)+\phi(z′)−2\phi(x′)=log|x|+log|z′|−2log|x′|$

我们将log合并，得到：

$\phi(x)+\phi(z′)−2\phi(x′)=log(\frac{|x||z′|}{|x′|^2})$

由于$|x′|≥a+b$（可以结合旋转过程思考一下），而$log$是单调的，因此：

$\phi(x)+\phi(z′)−2\phi(x′)≤log(\frac{ab}{(a+b)^2})≤log(\frac{ab}{2ab})≤−1$

证明完毕。现在我们已经知道zig−zig操作的摊还代价不大于：

$O(1)+\phi(x′)+\phi(z′)−2\phi(x)$

其中O(1)为旋转操作的复杂度。由于之前的推导我们可以知道\phi(x)+\phi(z′)−2\phi(x′)≤−1，因此−1−$(\phi(x)+\phi(z′)−2\phi(x′))≥0$，我们在摊还代价上加上这个非负数得到：

$O(1)+\phi(x′)+\phi(z′)−2\phi(x)−1−(\phi(x)+\phi(z′)−2\phi(x′))$

化简一下，就得到：

$O(1)+O(\phi(x′)−\phi(x))−1$

通过增大我们刚刚加的那个非负数以及势的单位，我们就可以支配隐藏在O(1)中的常数，因此一次zig−zig操作的摊还代价为：

$O(\phi(x′)−\phi(x))$

3、zig−zag操作

img
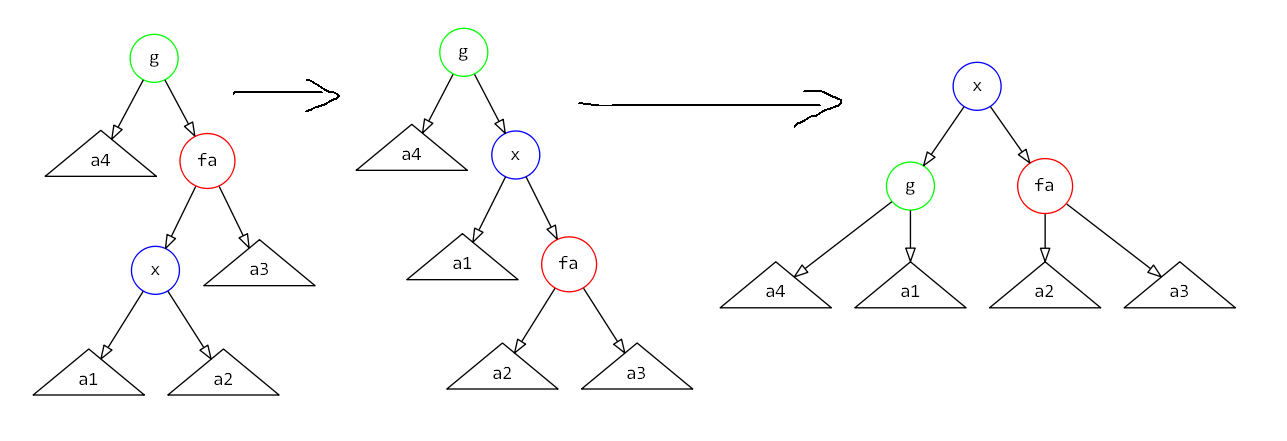
分析的过程和zig−zig操作完全一样，之前分析用到的所有性质此时仍然适用，因此略过分析过程。其摊还代价依然为：

$O(\phi(x′)−\phi(x))$

4、总结

综上所述，除了最后一次旋转可能增加$O(1)$的代价以外，其余操作的摊还代价只和我们伸展的对象$x$的势有关。我们假设旋转操作一共执行了$n$次，并用xi来表示节点x在经过i次旋转后的状态，那么整一个伸展操作的摊还代价就为：

$O(1+\sum{i=1}^n\phi(x_i)−\phi(x{i−1}))$

显然除了$\phi(x_n)$与$\phi(x_0)$外，所有的势都被抵消了，因此摊还代价为：

$O(1+\phi(x_n)−\phi(x0))$

至此，我们不必关心$\phi(x_0)$的值了。此时$x_n$是整棵Splay的根，因此$\phi(x_n)=log|T|$。我们成功的证明了一次伸展操作的摊还代价为$O(log|T|)$。

但是我有个问题就是整个分析根本不考虑Splay时旋转操作的顺序，换句话说就是不考虑单双旋，好像只要上述任意一组旋转都能这么分析？…不过暂时就这样先咕咕咕这个问题了

辅助树

  • 我们刚才在说的建树方法，其实就是辅助树的建树方法，我们先来 看⼀看辅助树的一些性质，再通过一张图实际了解一下辅助树的具体结构。
  • 每⼀个 Splay 维护的是一条路径，并且在原树中所有节点深度严格递增，并且，中序遍历这棵 Splay 得到的点序列列的点深度严格递增（即Splay按照深度为键值建树）。
  • 每个节点包含且仅包含于一棵 Splay 中。
  • ⼀棵 Splay 的根节点的 Father 指向它在辅助树中的父亲结点。但是它父亲结点的 ch 并没有指向这个点的。即父亲不不⼀定认⼉子，⽽⼉子能找到⽗亲。
  • 由于 LCT 的 Access 操作（后面会解释），使得 3. 中的⽗亲不认⼉子对答案⽆任何影响，同时，也使一些叶⼦结点单独构成一棵 Splay 辅助树成为可能
  • 由于辅助树的以上性质，我们维护任何操作都不需要维护原树，辅助树可以在任何情况下拿出一个唯一的原树，我们只需要维护辅助树即可。

在本文里，你可以认为一些 Splay 构成了一个辅助树，每棵辅助树维护的是一棵树，一些辅助树构成了 LCT，其维护的是整个森林。

一个Example

img

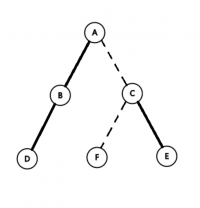
它的辅助树应该是这样的

img

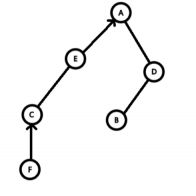
考虑原树和辅助树的结构关系

原树中的实链 : 在辅助树中节点都在一棵 Splay 中

原树中的虚链 : 在辅助树中，子节点所在 Splay 的 Father 指向父节点，但是父节点的两个儿子都不指向子节点。

注意：原树的根 ≠ 辅助树的根。

原树的 Father 指向 ≠ 辅助树的 Father 指向。

辅助树是可以在满足辅助树、Splay 的性质下任意换根的。

虚实链变换可以轻松在辅助树上完成，这也就是实现了动态维护树链剖分。

一颗Splay的根节点指向的点是这颗Splay里深度最浅的点在原树上的父亲对应的辅助树的点

接下来要用到的变量声明

  • ch[N][2] 左右⼉子
  • f[N] ⽗亲指向
  • sum[N] 路径权值和
  • val[N] 点权
  • tag[N] 翻转标记
  • laz[N] 权值标记
  • Other_Vars

函数声明

⼀般数据结构函数（字面意思）

  1. $PushUp(x)$
  2. $PushDown(x)$

Splay 系函数（不会多做解释）

  1. $Get(x) $获取 x 是父亲的哪个⼉子。
  2. $Splay(x) $通过和 Rotate 操作联动实现把 x 旋转到当前 Splay 的根。
  3. $Rotate(x)$ 将$ x $向上旋转一层的操作。

新操作

  1. $IsRoot(x)$ 判断当前节点是否是所在 Splay 的根
  2. $Access(x) $把从根到当前节点的所有点放在⼀条实链里，使根到它成为一条实路径，并且在同一棵 Splay 里里。
  3. $Update(x)$ 在$ Access $操作之后，递归的从上到下 $Pushdown $更新信 息。
  4. $MakeRoot(x)$ 使 x 点成为整个辅助树的根。
  5. $Link(x, y)$ 在 $x, y$ 两点间连⼀一条边。
  6. $Cut(x, y)$ 把$ x, y $两点间边删掉。
  7. $Find(x)$ 找到$ x$ 所在的$ Splay $的根节点编号。
  8. $Fix(x, v) $修改 $x$ 的点权为$ v$。
  9. $Split(x, y) $提取出来$ x, y $间的路路径，⽅方便便做区间操作

函数实现

$PushUp(x)$(严格$O(1)$)

1
2
3
inline void pushup(int x){
	s[x] = s[ch[0][x]] ^ s[ch[1][x]] ^ v[x];
}

下推取反标记也不可少

$pushrev(x)$

1
2
3
inline void pushrev(int x){
	std::swap(ch[0][x] , ch[1][x]) , rev[x] ^= 1;
}

$PushDown(x)$(严格$O(1)$)

1
2
3
4
5
6
7

inline void PushDown(int p) {
  if (__tag1[p] != std_tag1) {
    < do ls & do rs > 
    __tag1[p] = std_tag1;
  }
}

$Splay(x) \and Rotate(x)$ (均摊$O(logn)$)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#define Get(x) (ch[f[x]][1] == x)
inline void rotate(int x)
{
	int y = f[x] , z = f[y] , k = ch[1][y] == x , sn = ch[!k][x];
	if(nroot(y)) ch[ch[1][z]==y][z] = x ;
   	ch[!k][x] = y , ch[k][y] = sn;
	if(sn) f[sn] = y ;
   	f[y] = x , f[x] = z;
	pushup(y);
}
inline void splay(int x)
{
	int y = x , z = 0;
	st[++z] = y;
	while(nroot(y)) st[++z] = y = f[y];
	while(z) pushdown(st[z--]);
	while(nroot(x))
	{
		y = f[x] , z = f[y];
		if(nroot(y))
			rotate((ch[0][y] == x)^(ch[0][z] == y)? x : y);
		rotate(x);
	}
	pushup(x);
}

以上大概都是前置知识非常简单的实现。。
接下来实现LCT的基础函数及功能函数

$isRoot(x)$(严格$O(1)$)
在前面我们已经说过，LCT 具有 如果一个儿子不是实儿子，他的父亲找不到它的性质
所以当一个点既不是它父亲的左儿子，又不是它父亲的右儿子，它就是当前 Splay 的根

1
#define isRoot(x) (ch[f[x]][0] != x && ch[f[x]][1] != x)

$Access(x)$(均摊$O(logn)$)

这是LCT的核心操作，后面的大部分操作都依赖于它。

我们需要让给定节点到当前根上的路径都是重边。我们想求解一条路径，而这条路径恰好就是我们当前的一棵 Splay

1
2
3
4
5
inline void access(int x)
{
	for(int y = 0 ; x ; y = x , x = f[x])
		splay(x) , ch[1][x] = y , pushup(x);
}

比如（其实我根本没看底下这个例子）
我们有这样一棵树，实线为实边，虚线为虚边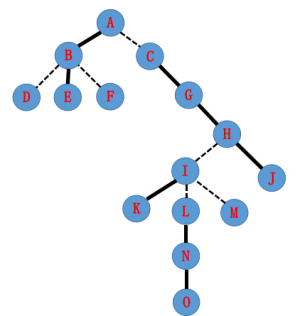
img
它的辅助树可能长成这样（构图方式不同可能 LCT 的结构也不同）
每个绿框里是一棵 Splay。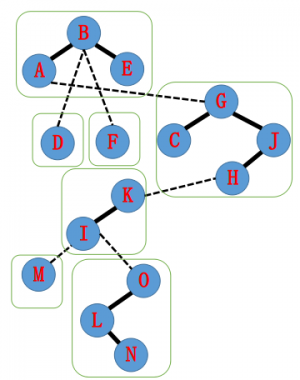
img

现在我们要 Access(N), 把 A-N 的路径都变实，拉成一棵 Splay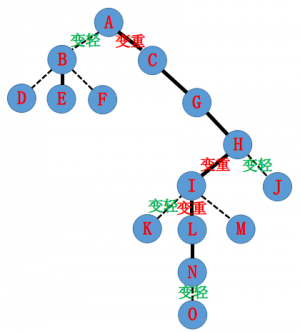
img

实现的方法是从下到上逐步更新 Splay
首先我们要把 N 旋至当前 Splay 的根。
为了保证 AuxTree 的性质，原来 N——O 的实边要更改为虚边。
由于认父不认子的性质，我们可以单方面的把 N 的儿子改为 Null。
于是原来的 Aux 就从下图变成了下下图。

img

img

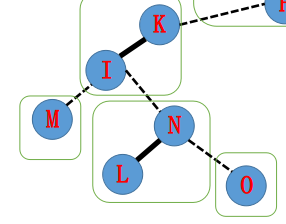
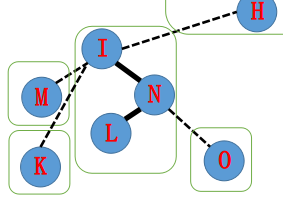
下一步，我们把 N 指向的 Father-> I 也旋转到它 (I) 的 Splay 树根。

原来的实边 I——K 要去掉，这时候我们把 I 的右儿子指向 N, 就得到了 I——L 这样一棵 Splay。

img

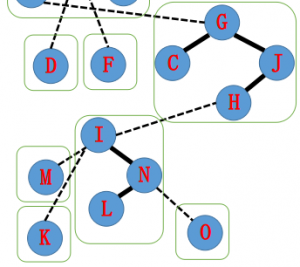
接下来，按照刚刚的操作步骤，由于 I 的 Father 指向 H, 我们把 H 旋转到他所在 Splay Tree 的根，然后把 H 的 rs 设为 I。

之后的树是这样的。

img

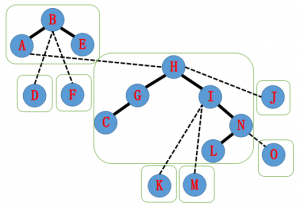
同理我们 Splay(A) , 并把 A 的右儿子指向 H。
于是我们得到了这样一棵 AuxTree。并且发现 A——N 的整个路径已经在同一棵 Splay 中了。大功告成！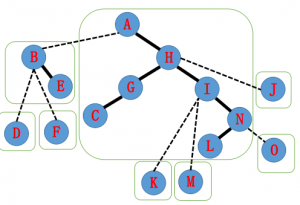
img

我们发现 Access() 其实很容易。只有如下四步操作：

  1. 把当前节点转到根。
  2. 把儿子换成之前的节点。
  3. 更新当前点的信息。
  4. 把当前点换成当前点的父亲，继续操作。

注意转Splay的顺序是按深度递增的，所以每次都是设置右儿子（我甚至想了一会）

UPD

这里似乎并不是很好懂，或者说我之后写代码发现又不明白了，所以我决定在这里说明这个做法到底是怎么一回事。

首先我们从$x$开始到上一颗Splay，然后这时$x$右儿子应该是不存在的因为在$x$的Splay中，它是最深的，Splay的键值就是深度。

后面的也好想，我们将一个点Splay到根后Splay的性质完全没有变化，这时我们跳到它的父亲$fx$，显然此时$fx$同样是Splay中的最深点（深度肯定是连续的，因为只隔了一条边），将它转到根上这个Splay也是正确的。

那么这两颗Splay应该在一起，怎么做呢？它的右儿子设为上一次Splay的根即可完成正确的合并，因为比当前的根深度大的点（即右儿子和右子树）显然不在$access$的路径中，所以右儿子应设置为深度大的Splay的根，这样中序遍历原先虚边链接的两个点是深度相邻的，这么做恰好就是相邻的。

其实这个不难想。主要是理解平衡树的中序遍历始终是有序的一个序列（这里就是按深度来的一个有序点集），然后我们把两个这东西合起来完全可以直接让根键值小的右儿子置为根键值大的Splay的根。平衡树没学好想半天退役吧

只需要说明两颗的情况，后面每一颗与之前的构成的两颗都相当于被归纳说明了。

真啰嗦

主要是不要忘了就好。

可以使用手工栈+迭代来减小常数

重要操作又来了

$makeroot(x)$

这个函数的作用是使LCT维护以$x$为根的树（森林）

$MakeRoot()$ 的重要性丝毫不亚于 $Access()$。我们在需要维护路径信息的时候，一定会出现路径深度无法严格递增的情况（也就是说LCA不是两点中的一个），根据 $Aux $的性质，这种路径是不能出现在一棵$ Splay $中的。
这时候我们需要用到$ MakeRoot()$。
$MakeRoot()$的作用是使指定的点成为原树的根，考虑如何实现这种操作。
我们发现$ Access(x) $后，$x$ 在$ Splay$ 中一定是深度最大的点（从根到 $x$, 深度严格递增）。
而变成根即是变成深度最小的点。我们 $Splay(x) $ , 发现这时候$ x $并没有右子树（即所有点深度都比它浅）。那我们把$ x $的左右儿子交换一下，变成了$ x $没有左子树，在 $Aux $意义上就是深度最小的点了，即达到目的。
所以我们交换左右儿子，并给右儿子打一个翻转标记即可。（此时左儿子没有值）。

整个流程：

  1. $Access(x)$
  2. $Splay(x)$
  3. tag(x) ^= 1(翻转标记)
    也就是说由于$x$经过$Access$后深度最大，所以我们把它$Splay$旋转到根，然后整条实链上的深度都反过来了，因为我们按照深度建树，所以相当于区间翻转了，打一个$Lazytag$即可。而其它实链是不需要处理的，它们并不受到影响，相对关系并没有变，也不需要做什么操作
    简单概括就是换根后其它实链上的点相对关系并没有变（他们之间的联系要么连在这条链上，要么连在其它链上，所以只需要处理这一条链即可）

浪费一下午想抛弃typora，结果失败了，活该，我爱typora一辈子

1
2
3
inline void makeroot(int x){
	access(x) , splay(x) , pushrev(x);
}

$findroot(x)$

用来查询实际树里的根，$link$和$cut$也需要判断连边是否合法。（map也行不过不一定快）

可以判断两点$x,y$是否在同一颗树里.先$Access(x)$ , 然后$find(y)$

1
2
3
4
5
6
7
inline int findroot(int x)
{
	access(x) , splay(x);
	while(ch[0][x]) pushdown(x) , x = ch[0][x];
	splay(x);
	return x;
}

$Link(x)$

$Link$ 两个点其实很简单，先 $Make_Root(x)$ , 然后把$ x $的父亲指向$ y $即可。显然，这个操作肯定不能发生在同一棵树内。记得先判一下。

1
2
3
4
5
inline void link(int x , int y)
{
	makeroot(x);
	if(findroot(y) != x) f[x] = y;
}

$cut(x ,y)$

注意一堆特判。

1
2
3
4
5
6
inline void cut(int x , int y)
{
	makeroot(x);
	if(findroot(y) == x && f[y] == x && !ch[0][y])
		ch[1][x] = f[y] = 0 , pushup(x);
}

$Split(x,y)$

有Splay维护区间基本经验应该就很容易接受。

先$Makeroot(x)$然后$Access(y)$，此时这条链已经在一个Splay中，在这个过程中时刻维护子树信息，（用最开头那个pushup和pushdown就可以）最后取根上的答案。

1
2
3
inline void split(int x , int y){
	makeroot(x) , access(y) , splay(y);
}

想起来很简单就是不知道写的时候怎么样了。

似乎LCT并不难，都是些很好理解的操作？

那你会证明复杂度吗？

正确性分析

这个数据结构各个操作的正确性似乎显然。。。

关于标记的正确性我也不知道该怎么说，就是对的。烦

复杂度分析

From Remoon

其实最好的证明是开头那篇原始论文的证明，比较懒就看的remoon的，不过思想好像是一样的。

我们只证明$Access(x)$的复杂度。（每个函数都会影响势能但是我们只需要分析一个，真神奇）

  1. 首先是在Splay中走的复杂度。

定义$w(x)=log2(|x|)$ ， $\varphi = \sum{x \in T}w(x)$

设它依次访问了$x_1,x_2….x_p$

那么，类似上文$splay$的复杂度分析，我们可以得到总的一次势能变化量为（为什么是加1啊）

他的势能改变量$\Delta \varphi = -w(x_1) + w(x_2) - w(x_2) + w(x_3)…… + w(x_p) + 1 \leq w(x_p) + 1 = O(logn)$

据说这叫Splay的finger-search性质。去看了下wiki

https://en.wikipedia.org/wiki/Finger_search

初始的势能也是需要考虑在内的。总复杂度为

$O((n+m)logn)$

  1. 访问更改虚边的复杂度

还是有时间看原版论文吧。

也许可以参考下Wiki？
https://en.wikipedia.org/wiki/Link/cut_tree

开头那篇是原版的，有点模糊。

找到一个分析上更简洁也更清楚的

LCT.pdf

和Wiki基本一样。

这个讲的就不错了，确实和remoon一样用的HLD来分析。

那我就懒得抄一遍markdown了

我甚至发现我有一份180页的Toptree论文，我知道我放了我也不会看的。

Design_and_Analysis_of_Data_Structures_for_Dynamic_Trees.pdf

代码

唯一的教训就是小心压行！！！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 300005

int st[maxn] , ch[2][maxn], f[maxn] , v[maxn] , s[maxn] , rev[maxn] , n , m;

inline bool nroot(int x){
	return ch[0][f[x]] == x || ch[1][f[x]] == x;
}

inline void pushup(int x){
	s[x] = s[ch[0][x]] ^ s[ch[1][x]] ^ v[x];
}

inline void pushrev(int x){
	std::swap(ch[0][x] , ch[1][x]) , rev[x] ^= 1;
}

inline void pushdown(int x)
{
	if(!rev[x]) return ;
	if(ch[0][x]) pushrev(ch[0][x]);
	if(ch[1][x]) pushrev(ch[1][x]);
	rev[x] ^= 1;
}

inline void rotate(int x)
{
	int y = f[x] , z = f[y] , k = ch[1][y] == x , sn = ch[!k][x];
	if(nroot(y)) ch[ch[1][z]==y][z] = x ;
   	ch[!k][x] = y , ch[k][y] = sn;
	if(sn) f[sn] = y ;
   	f[y] = x , f[x] = z;
	pushup(y);
}


inline void splay(int x)
{
	int y = x , z = 0;
	st[++z] = y;
	while(nroot(y)) st[++z] = y = f[y];
	while(z) pushdown(st[z--]);
	while(nroot(x))
	{
		y = f[x] , z = f[y];
		if(nroot(y))
			rotate((ch[0][y] == x)^(ch[0][z] == y)? x : y);
		rotate(x);
	}
	pushup(x);
}

inline void access(int x)
{
	for(int y = 0 ; x ; y = x , x = f[x])
		splay(x) , ch[1][x] = y , pushup(x);
}

inline void makeroot(int x){
	access(x) , splay(x) , pushrev(x);
}

inline int findroot(int x)
{
	access(x) , splay(x);
	while(ch[0][x]) pushdown(x) , x = ch[0][x];
	splay(x);
	return x;
}

inline void split(int x , int y){
	makeroot(x) , access(y) , splay(y);
}

inline void link(int x , int y)
{
	makeroot(x);
	if(findroot(y) != x) f[x] = y;
}

inline void cut(int x , int y)
{
	makeroot(x);
	if(findroot(y) == x && f[y] == x && !ch[0][y])
		ch[1][x] = f[y] = 0 , pushup(x);
}


inline void print()
{
	for(int i = 1 ; i <= n ; ++i)
		printf("%d ",s[i]);
}

int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&v[i]);
	for(int i = 1 ; i <= m ; ++i)
	{
	//	print();
		int op , x , y;
		scanf("%d%d%d",&op,&x,&y);
		if(!op) split(x,y) , printf("%d\n",s[y]);
		else if(op == 1) link(x,y);
		else if(op == 2) cut(x,y);
		else splay(x) , v[x] = y;
	}
}